Primin algoritmi

Tässä opetusohjelmassa opit, miten Primin algoritmi toimii. Löydät myös toimivia esimerkkejä Primin algoritmista C, C ++, Java ja Python.

Primin algoritmi on pienin ulottuva puu-algoritmi, joka ottaa kaavion syötteeksi ja löytää kaavion reunojen osajoukon, joka

muodosta puu, joka sisältää jokaisen kärjen
on pienin painojen summa kaikista puista, jotka voidaan muodostaa kaaviosta

Kuinka Primin algoritmi toimii

Se kuuluu ahneiksi algoritmeiksi kutsuttujen algoritmien luokkaan, jotka löytävät paikallisen optimin toivoen löytävänsä globaalin optimin.

Aloitetaan yhdestä kärjestä ja lisätään reunoja, joilla on pienin paino, kunnes saavutamme tavoitteemme.

Primin algoritmin toteuttamisen vaiheet ovat seuraavat:

Alusta pienin ulottuva puu pisteellä, joka on valittu satunnaisesti.
Etsi kaikki reunat, jotka yhdistävät puun uusiin pisteisiin, etsi minimi ja lisää se puuhun
Jatka vaiheen 2 toistamista, kunnes saamme vähimmäispituuden

Esimerkki Primin algoritmista

Aloita painotetulla graafilla

Valitse kärkipiste

Valitse pisteestä lyhin reuna ja lisää se

Valitse lähin kärkipiste, jota ei vielä ole ratkaisussa

Valitse lähin reuna, jota ei vielä ole ratkaisussa, jos valintoja on useita, valitse yksi satunnaisesti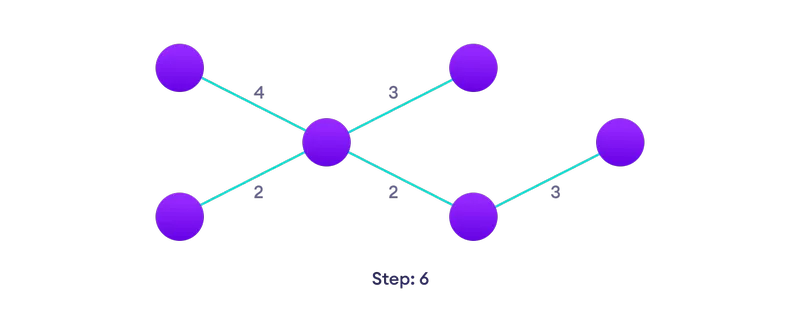

Toista kunnes on kattava puu

Primin algoritmin pseudokoodi

Primin algoritmin pseudokoodi osoittaa, kuinka luomme kaksi joukkoa pisteitä U ja VU. U sisältää luettelon käytetyistä kärkipisteistä ja VU luettelon pisteistä, joissa ei ole käynyt. Siirrämme yksi kerrallaan pisteitä joukosta UU sarjaan U kytkemällä pienin painoreuna.

 T = ∅; U = ( 1 ); while (U ≠ V) let (u, v) be the lowest cost edge such that u ∈ U and v ∈ V - U; T = T ∪ ((u, v)) U = U ∪ (v)

Python-, Java- ja C / C ++ -esimerkkejä

Vaikka kaavioiden vierekkäisyysmatriisiesitystä käytetään, tämä algoritmi voidaan toteuttaa myös Adjacency List -luettelolla sen tehokkuuden parantamiseksi.

Python Java C C ++

 # Prim's Algorithm in Python INF = 9999999 # number of vertices in graph V = 5 # create a 2d array of size 5x5 # for adjacency matrix to represent graph G = ((0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)) # create a array to track selected vertex # selected will become true otherwise false selected = (0, 0, 0, 0, 0) # set number of edge to 0 no_edge = 0 # the number of egde in minimum spanning tree will be # always less than(V - 1), where V is number of vertices in # graph # choose 0th vertex and make it true selected(0) = True # print for edge and weight print("Edge : Weight") while (no_edge  G(i)(j): minimum = G(i)(j) x = i y = j print(str(x) + "-" + str(y) + ":" + str(G(x)(y))) selected(y) = True no_edge += 1

 // Prim's Algorithm in Java import java.util.Arrays; class PGraph ( public void Prim(int G()(), int V) ( int INF = 9999999; int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false boolean() selected = new boolean(V); // set selected false initially Arrays.fill(selected, false); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in // graph // choose 0th vertex and make it true selected(0) = true; // print for edge and weight System.out.println("Edge : Weight"); while (no_edge < V - 1) ( // For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise // choose another vertex nearest to selected vertex at step 1. int min = INF; int x = 0; // row number int y = 0; // col number for (int i = 0; i < V; i++) ( if (selected(i) == true) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) System.out.println(x + " - " + y + " : " + G(x)(y)); selected(y) = true; no_edge++; ) ) public static void main(String() args) ( PGraph g = new PGraph(); // number of vertices in grapj int V = 5; // create a 2d array of size 5x5 // for adjacency matrix to represent graph int()() G = ( ( 0, 9, 75, 0, 0 ), ( 9, 0, 95, 19, 42 ), ( 75, 95, 0, 51, 66 ), ( 0, 19, 51, 0, 31 ), ( 0, 42, 66, 31, 0 ) ); g.Prim(G, V); ) )

 // Prim's Algorithm in C #include #include #define INF 9999999 // number of vertices in graph #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight printf("Edge : Weight"); while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) printf("%d - %d : %d", x, y, G(x)(y)); selected(y) = true; no_edge++; ) return 0; )

 // Prim's Algorithm in C++ #include #include using namespace std; #define INF 9999999 // number of vertices in grapj #define V 5 // create a 2d array of size 5x5 //for adjacency matrix to represent graph int G(V)(V) = ( (0, 9, 75, 0, 0), (9, 0, 95, 19, 42), (75, 95, 0, 51, 66), (0, 19, 51, 0, 31), (0, 42, 66, 31, 0)); int main() ( int no_edge; // number of edge // create a array to track selected vertex // selected will become true otherwise false int selected(V); // set selected false initially memset(selected, false, sizeof(selected)); // set number of edge to 0 no_edge = 0; // the number of egde in minimum spanning tree will be // always less than (V -1), where V is number of vertices in //graph // choose 0th vertex and make it true selected(0) = true; int x; // row number int y; // col number // print for edge and weight cout << "Edge" << " : " << "Weight"; cout << endl; while (no_edge < V - 1) ( //For every vertex in the set S, find the all adjacent vertices // , calculate the distance from the vertex selected at step 1. // if the vertex is already in the set S, discard it otherwise //choose another vertex nearest to selected vertex at step 1. int min = INF; x = 0; y = 0; for (int i = 0; i < V; i++) ( if (selected(i)) ( for (int j = 0; j G(i)(j)) ( min = G(i)(j); x = i; y = j; ) ) ) ) ) cout << x << " - " << y << " : " << G(x)(y); cout << endl; selected(y) = true; no_edge++; ) return 0; )

Primin vs. Kruskalin algoritmi

Kruskalin algoritmi on toinen suosittu vähimmäispinta-alan algoritmi, joka käyttää eri logiikkaa kaavion MST: n löytämiseen. Sen sijaan, että aloitettaisiin kärkipisteestä, Kruskalin algoritmi lajittelee kaikki reunat pienestä painosta suuriin ja lisää jatkuvasti alimmat reunat, ohittamatta syklin muodostavat reunat.